These instructions are based on the "Let's play chess" document published by the United States Chess Federation.

Chess is a game for two players, one with the "White" pieces and one with the "Black" pieces. At the beginning of the game, the pieces are set up as pictured below:

These hints will help you to remember the proper board setup:

1. Opposing Kings and Queens go directly opposite each other.
2. The square in the lower right hand corner is a light one ("light on right").
3. The White Queen goes on a light square, the Black Queen on a dark square ("Queen on color").

White always moves first, and then the players take turns moving. Only one piece may be moved at each turn (except for "castling", a special move that is explained later). The Knight is the only piece that can jump over other pieces. All other pieces move only along unblocked lines. You may not move a piece to a square already occupied by one of your own pieces. But you can capture an enemy piece that stands on a square where one of your pieces can move. Simply remove the enemy piece from the board and put your own piece in its place.

The Pieces and How They Move

The Queen

The Queen is the most powerful piece. She can move any number of squares in any direction - horizontal, vertical, or diagonal - if her path is not blocked. She can reach any of the squares with dots in the above diagram:

The Rook

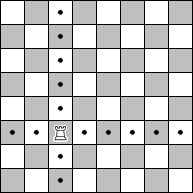
The Rook is the next most powerful piece. The Rook can move any number of squares vertically or horizontally if its path is not blocked.

The Bishop

The Bishop can move any number of squares diagonally if its path is not blocked. Note that this Bishop starts on a light square and can reach only other light squares. At the beginning of the game, you have one "dark-square" Bishop and one "light-square" Bishop.

The Knight

The Knight's move is special. It hops directly from its old square to its new square. The Knight can jump over other pieces between its old and new squares. Think of the Knight's move as an "L." It moves two squares horizontally or vertically and then makes a right-angle turn for one more square. The Knight always lands on a square opposite in color from its old square.

The King

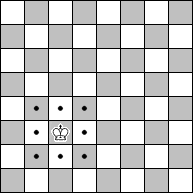
The King is the most important piece. When he is trapped, his whole army loses. The King can move one square in any direction - for example, to any of the squares with dots in this diagram. (An exception is castling, which is explained later). The King may never move into check - that is, onto a square attacked by an opponent's piece.

The Pawn

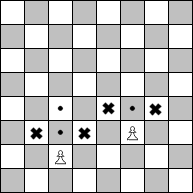
The pawn moves straight ahead (never backward), but it captures diagonally. It moves one square at a time, but on its first move it has the option of moving forward one or two squares. In the diagram, the squares with dots indicate possible destinations for the pawns. The pawn on the left is on its original square, so it may move ahead either one or two squares. The pawn on the right has already moved, so it may move ahead only one square at a time. The squares on which these pawns may capture are indicated by an X.

If a pawn advances all the way to the opposite end of the board, it is immediately "promoted" to another piece, usually a Queen. It may not remain a pawn or become a King. Therefore, it is possible for each player to have more than one Queen or more than two Rooks, Bishops, or Knights on the board at the same time.

Special Moves

Each player may "castle" only once during a game and when certain conditions are met. Castling is a special move that lets a player move two pieces at once — the King and one Rook. In castling, the player moves his King two squares to its left or right toward one of his Rooks. At the same time, the Rook involved goes to the square beside the King and toward the center of the board (see illustrations below). In order to castle, neither the King nor the Rook involved may have moved before. Also, the King may not castle out of check, into check, or through check. Further, there may not be pieces of either color between the King and the Rook involved in castling.

before Kingside Castling		after Kingside Castling
before Queenside castling		after Queenside Castling

Castling is often a very important move because it allows you to place your King in a safe location and also allows the Rook to become more active.

When the move is legal, each player has the choice of castling Kingside or Queenside or not at all, no matter what the other player chooses to do.

This French phrase is used for a special pawn capture. It means "in passing," and it occurs when one player moves a pawn two squares forward to try to avoid capture by the opponent's pawn. The capture is made exactly as if the player had moved the pawn only one square forward.

In the diagram, the Black pawn moves up two squares to the square with the dot. On its turn the White pawn may capture the Black one on the square marked with the X.

before En Passant capture		after En Passant capture

If the White player does not exercise this option immediately - before playing some other move - the Black pawn is safe from "en passant" capture for the rest of the game. But new opportunities may arise for each pawn in similar circumstances.

The main goal of chess is to checkmate your opponent's King. The King is not actually captured and removed from the board like other pieces. But if the King is attacked ("checked") and threatened with capture, it must get out of check immediately. If there is no way to get out of check, the position is a "checkmate", and the side that is checkmated loses.

You may not move into check. For example, moving into a direct line with your opponent's Rook, when if there are no other pieces between the Rook and your King, is not a legal move. Otherwise, the Rook could "capture" the King, which is not allowed.

If you are in check, there are three ways of getting out:

1. Capturing the attacking piece;
2. Placing one of your own pieces between the attacker and your King (unless the attacker is a Knight);
3. Moving the King away from the attack.

If a checked player can do none of these, he is checkmated and loses the game.

If a King is not in check, but that player can make no legal move, the position is called a stalemate and the game is scored as a draw, or tie.

How to Read and Write Chess

There are many different ways to write chess moves. The notation used at QueenAlice.com (also the most widely used in tournaments) is called algebraic notation and is described below.

The notation begins by identifying each square of the chessboard with a unique coordinate. First, the files (that is, lines running parallel to the direction the players are facing) are labelled with lowercase letters a through h, from the left of the "white" player. So the "a" file is to white's left, and to black's right. Then the ranks (lines running horizontally between the players) are numbered from 1 to 8, starting from white's home rank. Thus, black's home rank is rank 8. Each square of the board, then, is uniquely identified by its file letter and rank number. The white king, for example, starts the game on square e1. The black knight on b8 can move to a6 or c6 (or d7, if that square is vacant).

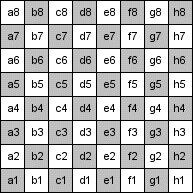
Each type of piece (with the exception of pawns) is identified by an uppercase letter. English speaking players use K for king, Q for queen, R for rook, B for bishop, and N for knight (since K is already used). The letters are different for other languages. At QueenAlice.com only the English letters are used.

Pawns are not indicated by a letter, but by the absence of such a letter - it is not necessary to distinguish between pawns for normal moves, as only one pawn can move to any one square (captures are indicated differently; see below).

Each move of a piece is indicated by the piece's initial, plus the coordinate of the destination square. For example Be5 (move a bishop to e5), Nf3 (move a knight to f3), c5 (move a pawn to c5--no initial in the case of pawn moves).

When a piece makes a capture, an x is inserted between the initial and the destination square. For example, Bxe5 (bishop captures the piece on e5). When a pawn makes a capture, the file from which the pawn departed is used in place of a piece initial. For example, exd5 (pawn on the e-file captures the piece on d5). En passant captures are specified by the capturing pawn's file of departure, the x, and the square to which it moves (not the location of the captured pawn).

If two identical pieces can move to the same square, the piece's initial is followed by: (1) if both pieces are on the same rank, the file of departure; (2) if both pieces are on the same file, the rank of departure. If pieces are on different ranks and files, method (1) is preferred. For example, with two knights on g1 and d2, either of which might move to f3, the move is indicated as Ngf3 or Ndf3, as appropriate. With two knights on g5 and g1, the moves are N5f3 or N1f3. As above, an x may be used to indicate a capture: for example, N5xf3. It may be necessary to identify a departing piece with both its file and its rank in unusual configurations (e.g. the player has 3 queens or 3 knights on the board). It is never necessary to specify that a capture was en passant because a capture from the same file but not en passant would have a different destination square.

If a pawn moves to its last rank, achieving promotion, the piece chosen is indicated after the move, followed by an "=" sign, for example e1=Q, b8=N.

Castling is indicated by the special notations O-O (for kingside castling) and O-O-O (queenside).

A move which places the opponent's king in check has the notation "+" added. Checkmate is likewise indicated by "#".